问题：

　　假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。

　　（这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个顶点，不相容活动间用边相连。使相邻顶点有不同颜色的最小着色数，相应于要找的最小会场数。）

数据输入：

　　第一行表示有 n 个活动。

　　接下来 n 行中，第 i 行的第一个数表示该活动的开始时间，第二个数表示该活动的结束时间。

数据输入：

输出最少需要的会场数。

思路：

　　将n个活动1，2，....，n看做实直线上的n个半闭活动区间（s[i]，f[i]]）。

　　所讨论的问题实际上是求这n个半闭区间的最大重叠数。

　　因为重叠的活动区间所相应的活动是互不相容的。若这n个活动区间的最大重叠数为m，则这m个重叠区间所对应的活动互不相容，因此至少要安排m个会场来容纳这m个活动。

　　如图：

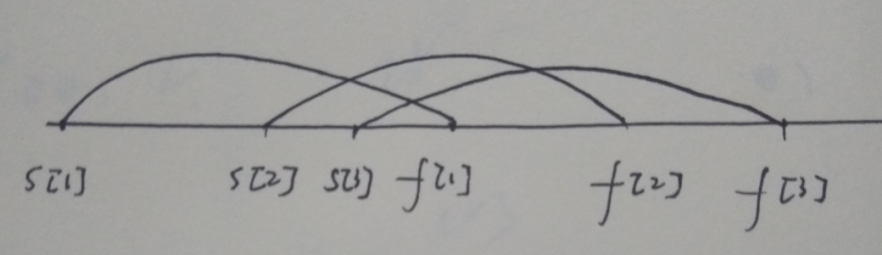将所有的时刻（开始的，结束的）按顺序排在一条线上，然后从这条线的开头往后面走，遇到的时刻是开始的话，重叠数就+1，遇到的时刻是结束的话，重叠数就-1.

代码：

#include<iostream>
#include<fstream>
using namespace std;

struct activity {
    int time;    //记录一个时刻
    bool f;    //表示这个是开始时刻还是结束时刻
};


void quickSort(activity s[], int l, int r)
{//快速排序函数，这个不是重点
    if (l < r)
    {
        int i = l, j = r;
        activity x = s[l];
        while (i < j)
        {
            while (i < j && s[j].time >= x.time)
                j--;
            if (i < j)
                s[i++] = s[j];

            while (i < j && s[i].time < x.time)
                i++;
            if (i < j)
                s[j--] = s[i];
        }
        s[i] = x;
        quickSort(s, l, i - 1);
        quickSort(s, i + 1, r);
    }
}

int activityPlan(activity a[], int l)
{//会场安排函数
    int overlap = 0, halls = 0;    //overlap 表示重叠数，halls表示需要的最少的会场数
    for (int i = 1; i <= l; i++)
    {
        if (a[i].f == true)
        {//遇到开始时间
            overlap++;
            if (overlap > halls)
            {//会场数即最大的重叠数
                halls = overlap;
            }
        }
        else
        {//遇到结束时间
            overlap--;
        }
    }
    return halls;
}

void main()
{
    ifstream input("input.txt");
    ofstream output("output.txt");

    int n, t;
    activity a[99];

    input >> n;

    //输入
    for (int i = 1; i <= 2 * n; i++)
    {
        input >> a[i].time;
        if (i % 2 == 1) a[i].f = true;
        else  a[i].f = false;
    }

    //先对输入的所有时刻进行排序
    quickSort(a, 1, 2 * n);

    output << activityPlan(a, 2 * n) << endl;

    input.close();
    output.close();
}