分析：

中间可断开

从题目中我们可以看到几个有用的量：x串的长度m，y的长度n

那么我们就可以用r[m][n]表示长度为m的串x和长度为n的串y的最长公共子序列的长度

问题一般化了就是：r[i][j]表示长度为i的串和长度为j的串的最长公共子序列的长度

然后递归地定义解就可以表示成：

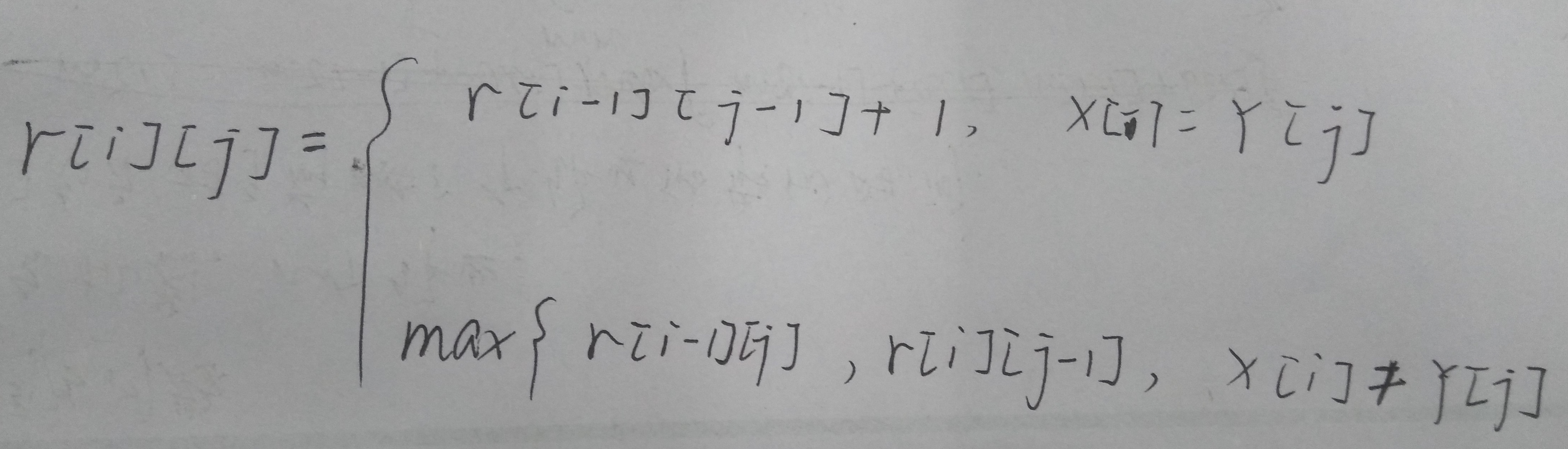
而反递归的动态规划的做法就是从最短的开始

代码：

    public static int ggzc(String A, int n, String B, int m) {
        int[][] r = new int[n + 1][m + 1];
        for (int i = 0; i < n; i++) {
            r[i][0] = 0;
        }
        for (int i = 0; i < m; i++) {
            r[0][i] = 0;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (A.charAt(i - 1) == B.charAt(j - 1)) {
                    r[i][j] = r[i - 1][j - 1] + 1;
                } else {
                    if (r[i - 1][j] > r[i][j - 1]) {
                        r[i][j] = r[i - 1][j];
                    } else {
                        r[i][j] = r[i][j - 1];
                    }
                }
            }
        }
        return r[n][m];
    }

中间不可断开：

 public static int findLongest(String A, int n, String B, int m) {
        // write code here
        int[][] r = new int[n + 1][m + 1];
        int max = 0;
        for (int i = 0; i < n; i++) {
            r[i][0] = 0;
        }
        for (int i = 0; i < m; i++) {
            r[0][i] = 0;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (A.charAt(i - 1) == B.charAt(j - 1)) {
                    r[i][j] = r[i - 1][j - 1] + 1;
                    if (max < r[i][j]) {
                        max = r[i][j];
                    }
                }
            }
        }

        return max;
    }